SAT Math Strategies That Actually Work
Math is one of two sections on the SAT (split into two modules just like its counterpart, Reading & Writing) and accounts for half of the total composite score—a maximum of 800 points out of the 1600 it's possible to earn. The content tested is drawn from a relatively small band of concepts: students who have taken Geometry and Algebra II in school will have encountered most if not all of the material that appears in the two SAT Math modules.
It's important to note, however, that this section is not simply a test of your math content knowledge; in fact, it's not a stretch to say that it's not even primarily a test of your math content knowledge. Rather, SAT Math will use these math concepts to assess your pattern recognition, flexible problem-solving skills, and critical reasoning.
This can make SAT Math seem very intimidating, and there's no avoiding the fact that it's a challenging section; however, it can be beaten! In this post, I'll take you through some of the most important tips and tricks to remember as you strive to conquer the SAT Math section. Let's get started.
Tip 1: Know the Section Layout, and Pace Yourself Accordingly
Each Math module on the SAT is composed of 22 questions; most of them are multiple choice, but pairs of 'student-produced response questions' are interspersed throughout. These problems do not give you answer choices to choose from, but rather require you to type in your answer directly. (Moving forward, I'll refer to these as manual-entry questions, or grid-ins—a holdover from the paper-and-pencil SAT, when the test actually gave you a numerical grid to bubble in your answer. No, I'm not super old, why do you ask?)
Additionally, each SAT Math module scales in terms of difficulty. This doesn't necessarily mean that question #15 will be harder than #14, which is harder than #13, etc.—one of the SAT's favorite tricks is to put a very difficult question earlier in the module than it should be located, in an attempt to intimidate you and throw off your rhythm. It does mean, though, that #18-22 will feel noticeably more difficult on average than #1-5.
So why do we care about all of this? In a word: timing. You're given 35 minutes to complete the 22 questions in each module, which translates to roughly 1 minute 35 seconds per question. You should expect, however, that the questions at the end of the module will take you longer than those at the beginning, which means that you need to allot more time to tackle those harder questions.
Question format matters here, too. You have a ¼ chance of correctly guessing even the hardest SAT multiple-choice question ever created by simply closing your eyes and clicking one of the choices. On the flip side, your chances of guessing a manual-entry question correctly are so small that they're functionally zero (I started to do the math there, but I'm not getting paid by the hour, so we're going with 'functionally zero'). This means that you should never get stuck guessing on a grid-in problem because you ran out of time; if you know you're going to be short on time, skip ahead to the grid-ins and prioritize them over the remaining multiple-choice questions.
Tip 2: Take a Multi-Pass Approach
One way to ensure that you're managing your time optimally is to work through the Math modules in stages. On your first pass through a module, focus on answering the problems where you read the question and think, "I know how to do this." If you don't have that sense of immediately knowing where to start, or if it seems like a very time-consuming question, flag it and move on. This way, you know that you've locked in the points that are easiest for you—the ones that you "should" get.
Once you've completed your first pass, it's time to tackle the rest of the module. It might make sense to go ahead and knock out any remaining grid-in questions first, for the reason that we discussed above. Note that you may not know the answer to every grid-in problem—some of them are of course more difficult than others—and that's totally okay; the goal is just to ensure that you're not leaving points on the board due to poor time management. Don't be so determined to answer every manual-entry question that you tank your timing on the rest of the module; that kind of defeats the purpose.
By structuring your progress through the section in this way, you ensure that any problems you have to guess on due to time constraints are A) the most difficult ones for you, meaning they're the points you were least likely to get anyway; and B) mostly multiple-choice questions, meaning you still have a ¼ chance of getting each point regardless.
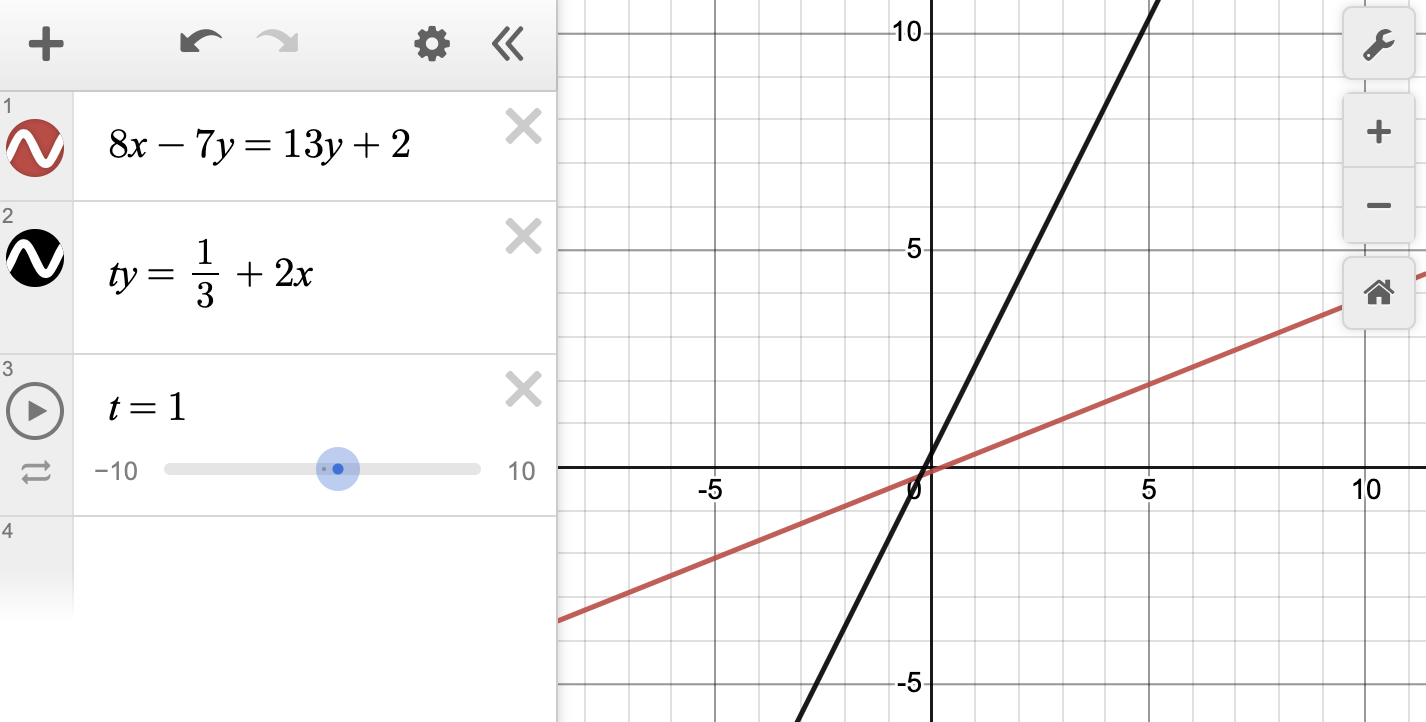
Tip 3: Desmos, Desmos, Desmos
By this point, you've probably run into videos on TikTok or YouTube with titles like "How to Use Desmos to Answer EVERY SINGLE QUESTION ON THE SAT". This is a bit of an exaggeration—marking the first time in recorded history that someone on the internet has given inaccurate information—but there's no denying that the Desmos graphing calculator built into the SAT testing client is an extremely powerful tool.
I'm not going to go into exhaustive detail on every single Desmos technique in this post, both because we'll be focusing on that in a separate future post and because you simply don't need to know all of them. Suffice it to say that if you're someone with a brain for hotkeys and keyboard shortcuts, you can get Desmos to do a substantial amount of heavy lifting for you in this section. Unless you already have a high degree of familiarity with that world, however, it's going to take significant practice and memorization to get to that point, and you're better off just spending that time reviewing math concepts you've already learned.
In terms of general tips, here are some of the areas where Desmos tends to be a huge time-saver for the average student who doesn't somehow already have a degree in computer science:
- Systems of equations: It's almost always faster to solve these by graphing rather than by using algebra.
- Graph anatomy: If a question asks you for the vertex of a parabola, for instance, put the equation into Desmos and look at it.
- Function transformations: Define your function in Desmos, then apply the transformation to it and use that graph to answer the question.
- Equivalent expressions: If two expressions are equivalent, they will produce the same graph. Compare the expression in the problem to the expression in each answer choice and see which one matches.
Tip 4: Look for Opportunities to Plug In
Our final foundational tip for the SAT Math section concerns every tutor's favorite technique: plug-ins. There are two basic types of plug-in strategy:
Answer plug-ins are best used when the question is asking you to find a single numerical quantity, such as the value of a variable.
Ex: If \( 4(x - 2)^2 + 11 = 5x \), what is a possible value of \( x \)?
A) \( -2 \)
B) \( 0 \)
C) \( \frac{5}{4} \)
D) \( \frac{9}{4} \)
We can solve this algebraically, and that may even be the fastest way to answer the question if you're a black belt in algebra; however, we can also plug the number in each answer choice in for \( x \) in the question equation, do some quick math, and find the number that balances the equation. As a bonus, you can even combine this strategy with Tip 3 to get Desmos to do the plug-in math for you.
Variable plug-ins can be applied to questions where the answer depends on the value of a particular variable.
Ex: Which of the following expressions is equivalent to \( (y - 5)^3 \)?
A) \( y^3 + 15y^2 + 75y - 125 \)
B) \( y^3 + 15y^2 - 75y - 125 \)
C) \( y^3 - 15y^2 + 75y - 125 \)
D) \( y^3 - 15y^2 - 75y - 125 \)
Again, we can use our flawless algebra mechanics to rewrite the question expression in the form of the answer expressions and then compare them. Some students, though, might find it easier to take an alternate route and do some plugging in.
To start, we need to recognize that we're given no restrictions on the value of our variable \( y \). This means that we can plug in our own number—say, 2—and evaluate the question expression using that input:
\[ ((2) - 5)^3 = (-3)^3 = -27 \]
Then, we'll compare that result to what we get when we plug 2 into each answer expression for \( y \). Whichever answer expression is equivalent to the question expression will produce the same output when given the same input:
\[ \text{C)} \quad (2)^3 - 15(2)^2 + 75(2) - 125 = 8 - 60 + 150 - 125 = \mathbf{-27} \]
The end result is that we can earn a point on this question without doing a bit of algebra.
It's perfectly normal for students to feel intimidated and a bit overwhelmed when faced with the SAT Math section for the first time. Even when you recognize the concept(s) that show up in a particular question, it's highly unlikely that the material is going to be tested in the same way it was in math class at school.
The key is to recognize that this section, and the SAT as a whole, has its own patterns, propensities, and proclivities. To succeed on the test, you need to recognize those trends and look for ways to take advantage of them. Hopefully this post gives you a good starting point for doing just that—and if you're looking for additional support on the SAT, we'd love to help you out!